
The argument x of f( x) is replaced by − x. And every point that was on the left gets reflected to the right. To reflect the absolute value function over the x-axis, we simply put a negative sign before the symbol (in this case the absolute value bars). Every point that was to the right of the origin gets reflected to the left. So, image equation of the given equation is 2x+3y -8. Every y-value is the negative of the original f( x).įig. Solution : Required transformation : Reflection about y - axis, So replace x by -x. That is: In other words, a reflection over the y- axis will be given by: To shift horzontally, we add if we are moving. To reflect a function over the y- axis, we multiply the input by a negative. Its reflection about the x-axis is y = − f( x). We are given the parent function: And we want to find the equation after a reflection in the y- axis followed by a translation of three units right. Only the roots, −1 and 3, are invariant.Īgain, Fig. And every point below the x-axis gets reflected above the x-axis.

Every point that was above the x-axis gets reflected to below the x-axis.
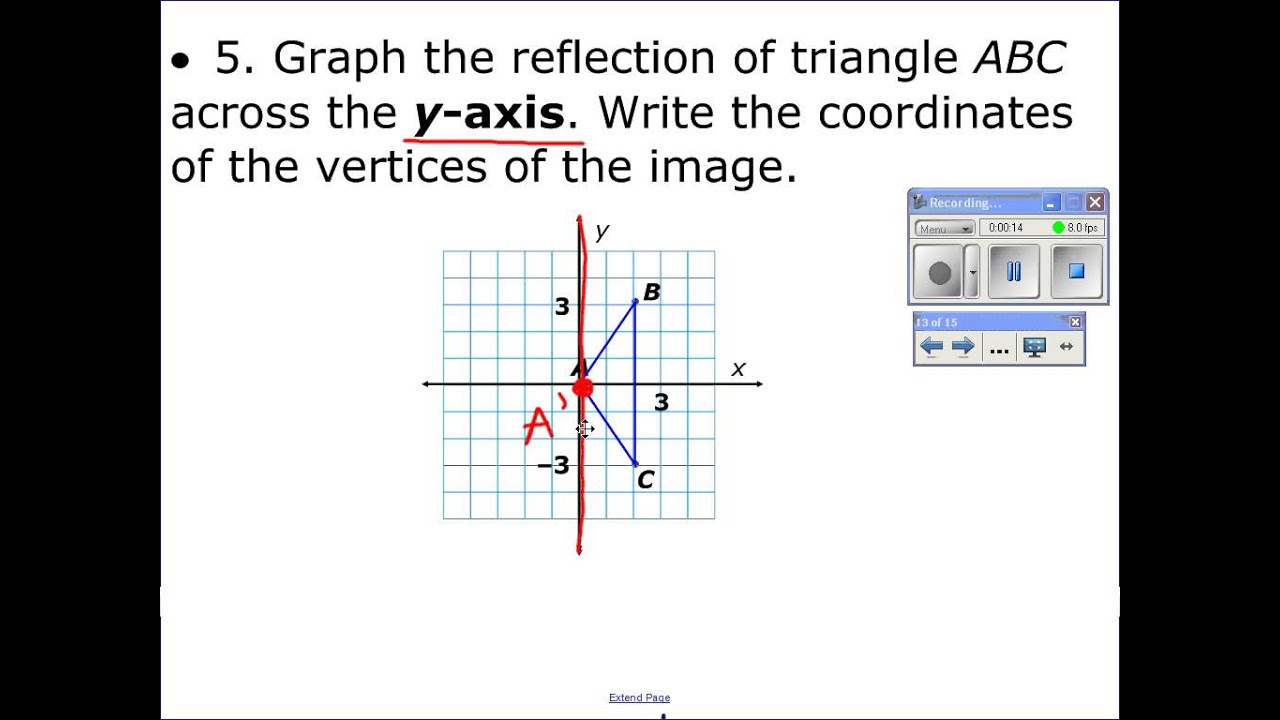
The distance from the origin to ( a, b) is equal to the distance from the origin to (− a, − b).į( x) = x 2 − 2 x − 3 = ( x + 1)( x − 3).įig. Reflection over the y-axis A reflection in the y-axis can be seen in diagram 4, in which A is reflected to its image A.
If we reflect ( a, b) about the x-axis, then it is reflected to the fourth quadrant point ( a, − b).įinally, if we reflect ( a, b) through the origin, then it is reflected to the third quadrant point (− a, − b). It is reflected to the second quadrant point (− a, b). Making the output negative reflects the graph over. C ONSIDER THE FIRST QUADRANT point ( a, b), and let us reflect it about the y-axis. The best way to practice drawing reflections over y axis is to do an example problem: Example: Given the graph of y f (x) yf(x) y f (x) as shown, sketch y f ( x) y f(-x) y f ( x). We can also reflect the graph of a function over the x-axis (y 0), the y-axis(x 0), or the line y x.


 0 kommentar(er)
0 kommentar(er)
